Using Computer Vision to Find Out How Bad I Am at Set

I bought Set after watching the Numberphile video covering it, and quickly realized that, playing solo, I had no way of knowing how good I was at identifying sets. If there didn’t appear to be any sets in the twelve cards I’d dealt myself, I couldn’t tell whether there truly weren’t any, or if I just couldn’t find them. One way to be sure is to check all 220 (12 choose 3) combinations of cards to see if any form a set. This is a task which, done manually, would swiftly result in a forehead-shaped dent in my desk. Programming a computer to do it, on the other hand, ended up keeping me entertained for weeks.

The Game

Cards in Set consist of four features: the number of shapes on a card, the type of shape, their color, and their shading (all shapes on a single card will be identical). Each of these features have three possibilities: there can be one, two, or three shapes, which can be (what I call) pills, diamonds, and squiggles. They can be red, green, or purple, and their shading can be soild, striped, or empty. Three cards form a set if across each card, all features are either all the same or all different. For example, the three cards below form a set

as they are all solid shaded red, and they all have a different type and quantity of shape. On the other hand, the below cards do not form a set, as two are red and one is green:

The objective of the game is to identify sets as quickly as possible. When playing with others, the first one to correctly identify a set gains a point, and the three cards are replaced with cards drawn from the deck. When playing solo, I guess the objective is to keep finding sets until you get bored. I don’t know. I played the game once when I bought it and have been working on this project since then. Let’s talk about that.

Recognizing Cards

I used Python and OpenCV to take in images from a webcam, identify cards and their features, and determine if any three cards in the frame form a set. The first step is to pick out the cards themselves. For this, I used OpenCV’s Canny() and findContours() functions, which detect edges in a grayscale image and then find contours along those edges, respectively. After dilating and eroding the edges to avoid any errant breaks in the shape outlines, I obtained a decent result:

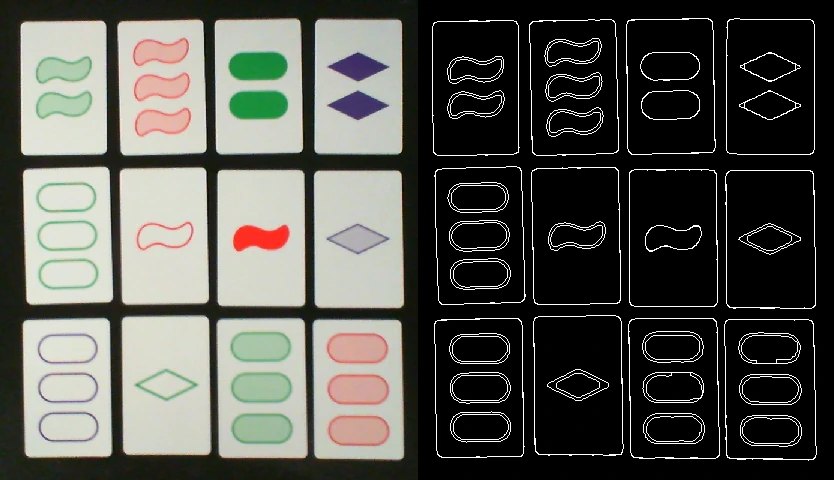
However, notice that shapes with empty or striped shading have two contours - one for the outside outline of the shape, and one for the inside. Furthermore, although not visible in the image, every contour has several duplicates, so we need a way to get exactly one contour for every actual contour in the image. Luckily, findContours() also returns a tree structure which tells us which contours are inside each other, so we can use the following algorithm:

1. Declare a dictionary cards. The keys of this dictionary will be the indices of each card outline in the contours array, and the values will be arrays containing the indices of each shape’s outline
2. Navigate to the top of the contour tree (this is where the card outlines will be)
3. Store the indices in the topmost level of the tree into a temporary card_idxs array
4. For each index i in card_idxs
   • While there is a next contour down in the tree
     • If the area of the next contour is less than 10% different from the area of the current contour, they represent the same underlying contour, so continue with the next contour down
     • Otherwise, the next contour is the outline of a shape, so store it and all of its neighbors in cards[i]

This way, we get the desired result

and len(cards[i]) gives us the number of shapes on each card i, which is our first feature!

One alternate solution is to use the RETR_EXTERNAL contour retrieval mode, which only retrieves the outermost contours. By doing this once to retrieve all the card outlines and then again for each card, we can avoid having to traverse the hierarchy. However, this would also create a separate contour array for each card, with all of the contour points needing to be translated back to their original coordinates. I’m sure the complexity of that solution is no worse than this one, but this is what I went with.

Discerning Shape Types

The first approach I took to distinguish shapes from one another was to match based on the shape’s perimeter or area. Unfortunately, there was too much similarity between the areas and perimeters of different shapes, so that approach proved unsuccessful. Even if it were, the thresholds for those values would need to be adapted based on the input image, as they vary with scale. I settled on comparing how well each shape is approximated by a polygon using OpenCV’s approxPolyDP() function (while writing this, I came across the matchShapes() function, which uses Hu invariants. This is likely a better solution and worth investigating).

The approxPolyDP() function takes the original contour and a value, called epsilon, that represents the maximum distance between the original contour and its approximation. It returns the polygon approximation. We run this twice: once to distinguish diamonds from pills and squiggles, and once more to distinguish pills from squiggles. By tweaking the two epsilon values of these passes and matching based on the number of points in the approximations, I was able to classify each shape with an acceptable degree of accuracy. Some frames lead to incorrect shape classification, but the majority are correct, which is enough to draw the user’s attention to a set they might not have noticed. See the video below, with (with what the program thinks are) diamonds drawn in red, pills in blue, and squiggles in green:

And thus the second feature is done. As previously mentioned, the matchShapes() function likely improves the accuracy with which shapes are distinguished from one another. Maybe I’ll get around to it, but this level of accuracy is satisfactory for now.

Determining Color

To determine the color of a shape, I settled on sampling the color of each point on the shape’s contour, taking a mean, and matching based on the hue of that mean. This method works, but has a couple downsides. Like the polygon approximation method above, not all frames are correctly matched. Furthermore, the hue thresholds need to be adapted based on the input frame (e.g. to adjust for different lighting). Nevertheless, the recognition is correct for most of the frames, and adding sliders for the hue thresholds makes them easy to adjust to obtain the desired results.

The results I got recording this demonstration are the best I’ve had so far for color recognition - I rarely have every single frame be correct. Now all that remains is to determine the shading of each shape.

Determining Shading

I initially tried a similar approach that I used for color detection to determine the card’s shading. By sampling the color at the center of a shape, I could match based on the saturation to determine if a shape is solid, striped, or empty. Unforunately, this method proved less reliable than it was for determining color. There was more overlap in the saturation values for different shadings, so finding a reliable threshold wasn’t possible. It was also sensitive to uneven lighting in the image. The solution to this problem lay in a concept in mathematics called metric spaces. I first came across the topic in my first Real Analysis class, in which I set a new personal all-time exam score low of 13/100. Still passed, though 😎.

In short, a metric space is a way to generalize the concept of distance. You can read into all the details on Wikipedia. Some easily understandable examples include the number line with the absolute difference metric (the distance between two numbers a and b is |a - b|), two-dimensional space with the Euclidean metric (the distance formula you learned in high school Geometry), or the space of all strings with the Levenshtein distance metric. A less easily understandable example is the space of all bounded functions on a set with the supremum norm, but that is of no concern to us.

Instead of considering the color in the center of the shape on its own, we can look at how different it is from the card’s background color. An empty shaded card should have close to no difference; a solid card should have a large difference, and a striped one should be somewhere in the middle. By looking at this problem through the lens of metric spaces, we can formulate a useful definition of “difference” in this context, and produce a significantly accurate result.

Colors in our image are represented in RGB (well, technically it’s BGR in OpenCV’s case, but it doesn’t make a difference here). These are just points in three-dimensional space, so we can use the three-dimensional distance formula to determine how close the sampled color is to the card’s background. We can sample the card’s backround from any point that we know won’t fall on a shape. I chose a spot in the top left corner.

Here’s a video showing the distance value for each shape. We see that there are clear boundaries between the distance values for different types of shading with no overlap. You can tell which shadings are which without even needing to see the input image.

Now that we’re able to reliably identify each of a card’s features, we can write an algorithm that determines when three cards form a set.

Finding Sets

The Numberphile video describes one approach to determining if three cards form a set. To summarize, we first assign a number from 0 to 2 to each possible feature state. Then, by summing across each feature of three cards, those cards form a set if and only if each sum is divisible by three. If a feature is all different across the cards, then the sum will be 0 + 1 + 2 = 3. If a feature is all the same, then the sum will be n + n + n = 3n for some n between 0 and 2. The proof of the converse is left as an exercise to the reader.

By encoding each card as a 4-dimensional vector of values as described above, we can sum them, take them modulo 3, and use numpy’s any() function to tell us if there are any nonzero values in the vector. This would mean that at least one of the sums modulo 3 is not equal to zero, so the sum is not divisible by 3, and the cards do not form a set.

def is_set_modulo(a, b, c):
    return not np.any((a + b + c) % 3)

All that’s left is to tell the user which cards, if any, form a set. I did this by simply giving the cards a yellow outline. Here’s a bird’s eye view of the final project:

# constants for representing card attributes as integers
consts = types.SimpleNamespace()
consts.ONE = 0
consts.TWO = 1
consts.THREE = 2

consts.DIAMOND = 0
# ...

# a class to hold a card's contour and attributes
# later we assign card.attributes = np.array([count, shape, color, shade])
class Card:
    def __init__(self, contour):
        self.contour = contour

# defined above
def is_set_modulo(a, b, c) -> bool

# takes in an input frame, and returns an array of Cards
def recognize_cards(frame) -> Card[]


while True:
    cap = cv.VideoCapture()
    while True:
        # get a frame from the camera
        ret, frame = cap.read()
        if ret:
            cards = recognize_cards(frame)

            if cards is None:
                continue

            # loop through all the combinations of three cards
            # (using the itertools package)
            for a, b, c in combinations(cards, 3):
                if is_set_modulo(a.attributes, b.attributes, c.attributes):
                    # outline each card in yellow using {a,b,c}.contour
                    break

            cv.imshow("frame", frame)

And the final result:

You might have noticed that the bottom-leftmost card is incorrectly identified as red in most of the frames. This demonstration was recorded in natural light coming from my window. I presume that that light is more uneven than the lamp I used when recording the other demos, which I did at night. I’ll accept this as an error in the input data, although I’m sure an improvement to the color detection method would also improve the accuracy.

And thus I have successfully written a program to tell me whether or not there is a set in the twelve cards laid out in front of me. As always, there are improvements to be made, and perhaps I’ll come back to this project and make them. At this point, however, I’m satisfied in calling the project done, as I’ve achieved my goal with it. You can view all the code on GitHub, including a sort of development journal I kept while working through the project, in case you’re interested in my raw, unfiltered thought process throughout the project.

Bonus: Alternate Set Finding Using Bitwise Operations

I came up with an alternate encoding/algorithm to determine if three cards form a set using bitwise operators. We can encode each card in 12 bits representing each feature as a set of three bit flags, like so:

000 000 000 000
|   |   |   |- count: 1 = 001, 2 = 010, 3 = 100
|   |   |----- shape: diamond = 001, pill = 010, squiggle = 100
|   |--------- color: red = 001, green = 010, purple = 100
|------------- shade: solid = 001, striped = 010, empty = 100

We now seek some ternary bitwise operation that produces zero when three cards form a set and nonzero otherwise. Then, all we have to do is apply that operation to the three cards and check if the result is zero. To find this operation, we can use a truth table. For each triplet, we want to produce 0 if the triplet is all the same or all different across three cards. It’s easier to consider the negation - we produce a 1 if two triplets are the same but one is different. For this to happen, there must be some position in the triplet where two bits are 1 and one is 0:

all triplets are either all the same or all different - we have a set!
100 100 100 100
100 010 010 010
100 001 001 001

the first triplet has two 100's and one 010 - not a set!
100 100 100 100
100 010 010 010
010 001 001 001
|- this bit has two 1s and one 0

So we construct our truth table:

| A | B | C | Product |
+---+---+---+---------+
| 0 | 0 | 0 |    0    |
| 0 | 0 | 1 |    0    |
| 0 | 1 | 0 |    0    |
| 0 | 1 | 1 |    1    |
| 1 | 0 | 0 |    0    |
| 1 | 0 | 1 |    1    |
| 1 | 1 | 0 |    1    |
| 1 | 1 | 1 |    0    |

This truth table tells us precisely what our bitwise operation will be: We want to produce a 1 either when A is 0, B is 1, and C is 1, or when A is 1, B is 0, and C is 1, or when A is 1, B is 1, and C is 0. Thus, our operation is

(~A & B & C) | (A & ~B & C) | (A & B & ~C)

Simplifying, we obtain

((A ^ B) & C) | (A & B & ~C)

where ^ denotes exclusive OR.

A cursory benchmark shows that this approach is slower than the sum mod 3 approach, even without numpy’s optimizations for vector operations:

def is_set_bitwise(a, b, c):
    return ((a ^ b) & c) | (a & b & ~c) == 0

# tested with 100 sets of three randomly generated integers from 0 to 0b111111111111 inclusive
# 10,000 trials
# bitwise: 145ns per execution

def is_set_modulo(a, b, c, d, e, f, g, h, i):
    return (a + b + c) % 3 == 0 and (d + e + f) % 3 == 0 and (g + h + i) % 3 == 0

# tested with 100 sets of nine randomly generated integers from 0 to 2 inclusive
# 10,000 trials
# modulo: 110ns per execution

This benchmark isn’t perfect, as the randomly generated data may not represent valid cards. However, it gives us a rough idea of how the two methods perform compared to each other. While the sum mod 3 method is faster, the bitwise method saves on the memory required to store the cards. Where the sum mod 3 approach requires at least 4 bytes per card - one for each integer representing a feature, the bitwise approach requires only 2 to store the required 12 bits. Practically speaking, the methods are identical. Finding a set 35 nanoseconds faster doesn’t matter when your camera is running at 60 frames per second, and at 81 cards in the deck, storing every card as 4 integers would take 324 bytes, which is chump change to any modern computer. Nevertheless, finding and benchmarking optimizations is fun, and a good skill to practice for when it actually does matter.